PageRank (PR) is an algorithm used by Google Search to rank websites in their search engine is used to find out the importance of a page to estimate how good a website is.
It is not the only algorithm used by Google to order search engine results.
In this topic I will explain
What is PageRank?
· Page rank is vote which is given by all other pages on the web about how important a particular page on the web is.
· A link to a page counts as a vote of support.
· The number of times a page is refers to by the forward link it adds up to the website value.
· The number of times it is taken as an input to the previous page it also adds up to the web value.
Simplified algorithm of PageRank:
Equation:
PR(A) = (1-d) + d[PR(Ti)/C(Ti) + …. + PR(Tn)/C(Tn)]
Where:
PR(A) = Page Rank of a page (page A)
PR(Ti) = Page Rank of pages Ti which link to page A
C(Ti) = Number of outbound links on page Ti
d = Damping factor which can be set between 0 and 1.
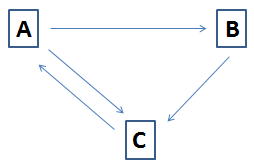
Let’s say we have three pages A, B and C. Where,
1. A linked to B and C
2. B linked to C
3. C linked to A
Calculate Page Rank:
Final Page Rank of a page is determined after many more iterations. Now what is happening at each iteration?
Note: Keeping
· Standard damping factor = 0.85
· At initial stage assume page rank of all page is equal to 1
Iteration 1:
Page Rank of page A:
PR(A) = (1-d) + d[PR(C)/C(C)] # As only Page C is linked to page A
= (1-0.85) + 0.85[1/1] # Number of outbound link of Page C = 1(only to A)
= 0.15 + 0.85
= 1
Page Rank of page B:
PR(B) = (1-d) + d[PR(A)/C(A)] # As only Page A is linked to page C
= (1-0.85) + 0.85[1/2] # Number of outbound link of Page A = 2 (B and C)
= 0.15 + 0.425 # and page rank of A was 1 (calculated from previous
= 0.575 # step)
Page Rank of page C:
· As Page A and page B is linked to page C
· Number of outbound link of Page A [C(A)] = 2 (ie. Page C and Page B)
· Number of outbound link of Page B [C(B)] = 1 (ie. Page C)
· PR(A) = 1 (Result from previous step not initial page rank)
· PR(B) = 0.575 (Result from previous step)
PR(B) = (1-d) + d[PR(A)/C(A) + PR(B)/C(B)]
= (1-0.85) + 0.85[(1/2) + (0.575/1)]
= 0.15 + 0.85[0.5 + 0.575]
= 1.06375
This is how page rank is calculated at each iteration. In real world it iteration number can be 100, 1000 or may be more than that to come up with final Page Rank score.
Implementation of PageRank in Python:
By networkx package in python we can calculate page rank like below.
import networkx as nx
import pylab as plt
# Create blank graph
D=nx.DiGraph()
# Feed page link to graph
D.add_weighted_edges_from([('A','B',1),('A','C',1),('C','A',1),('B','C',1)])
# Print page rank for each pages
print (nx.pagerank(D))
Output:
{'A': 0.38778944270725907, 'C': 0.3974000441421556, 'B': 0.21481051315058508}
# Plot graph
nx.draw(D, with_labels=True)
plt.show()
How PageRank works?
Official networkx documentation saying the PageRank algorithm takes edge weights into account when scoring.
Let’s test how it works. Let’s say we have three pages A, B and C and its graph as follows.
Weight matrix:
|
A
|
C
|
B
|
Out Link
|
|
|
A
|
0
|
2
|
3
|
5
|
|
C
|
1
|
0
|
0
|
1
|
|
B
|
0
|
1
|
0
|
1
|
Explain:
· Weight of A to B is 3 A to C is 2 and total number of out link of A =0+2+3 =5
· Weight of C to A is 1 C to B is 0 and total number of out link of C =1+0+0 =1
· Weight of B to A is 0 B to C is 1 and total number of out link of B =0+1+0 =1
So Weighted Score (WS) for:
· A-B = 3
· A-C = 2
· C-A = 1
· B-C = 1
Note: A-B implies to A to B
Equation:
PR(A) = (1-d)*p + d(x * WS(Ti)/C(Ti))
Where:
PR(A) = Page Rank of a page (page A)
WS(Ti) = Weighted Score of a page Ti
C(Ti) = Number of outbound links on page Ti
d = Damping factor which can be set between 0 and 1. (0.85 is default value)
p = Personalized vector which is ignorable
x = Initial page rank of a page = 1/3 for each page as total 3 pages we have.
Calculate WS(Ti)/C(Ti):
|
A
|
C
|
B
|
Out Link
|
A
|
C
|
B
|
|||
|
A
|
(0/5)
|
(2/5)
|
(3/5)
|
5
|
A
|
0
|
0.4
|
0.6
|
|
|
C
|
(1/1)
|
(0/1)
|
(0/1)
|
1
|
>>>
|
C
|
1
|
0
|
0
|
|
B
|
(0/1)
|
(1/1)
|
(0/1)
|
1
|
B
|
0
|
1
|
0
|
Calculate (x * WS(Ti)/C(Ti)):
|
A
|
C
|
B
|
A
|
C
|
B
|
|||
|
A
|
(0/5)*0.33
|
(2/5)*0.33
|
(3/5)*0.33
|
A
|
0
|
0.132
|
0.198
|
|
|
C
|
(1/1)*0.33
|
(0/1)*0.33
|
0*0.33
|
>>>
|
C
|
0.33
|
0
|
0
|
|
B
|
(0/1)*0.33
|
(1/1)*0.33
|
(0/1)*0.33
|
B
|
0
|
0.33
|
0
|
|
|
0.33
|
0.462
|
0.198
|
So from above:
(x * WS(Ti)/C(Ti)) value of A = 0.33
(x * WS(Ti)/C(Ti)) value of C = 0.462
(x * WS(Ti)/C(Ti)) value of B = 0.198
Now let’s calculate Page Rank:
Page Rank of A:
PR(A) = (1-d)*p + d(x * WS(Ti)/C(Ti))
PR(A) = (1-0.85) + 0.85(0.33) # Ignoring personalization factor(p)
= 0.15 + 0.2805
= 0.4305
Page Rank of C:
PR(A) = (1-d) + d(x * WS(Ti)/C(Ti))
PR(A) = (1-0.85) + 0.85(0.462) # Ignoring personalization factor(p)
= 0.15 + 0.3927
= 0.5427
Page Rank of B:
PR(A) = (1-d) + d(x * WS(Ti)/C(Ti))
PR(A) = (1-0.85) + 0.85(0.198) # Ignoring personalization factor(p)
= 0.15 + 0.1683
= 0.3183
Note: This all is just one iteration.In networkx package pagerank function have 100 iteration by default.
Conclusion:
In this article I have covered
· Overview of Page Rank
· What is Page Rank Algorithm
· How Page Rank Algorithm works
· Implementation of Page Rank Algorithm in Python by networkx package (pagerank function)
· How pagerank function of networkx package works.
Do you have any question?
Ask your question in the comment below and I will do my best to answer.


Nice Thanks for sharing
This really answered my problem, thank you!
Properly written post, properly researched and valuable for me in the future.I am so pleased you took the time and effort to create this. See you about
Man! You blow my mind by these summaries. Great article.
Thanks.
Thanks for sharing this type of depth post.
Great explanation of the PageRank algorithm and its implementation in Python! It’s a fundamental concept in search engine technology, and your breakdown of the equations and steps makes it easy to understand. Thanks for sharing this insightful article.